Jennifer Chang

Jennifer Chang

Her PhD was in Bioinformatics and Computational Biology with a minor in Statistics. During her PhD, she developed the C++ software Mango Graph Studio which has been licensed to a startup. Since then, she has worked on automating the Influenza A Virus in Swine reports and recently has been designing Nextflow pipelines for highly scalable and reproducible pipelines. She enjoys designing workflows to reduce tedium and increase joy of discovery.

Last Update: 14 Jan 2021
RMarkdown: R_Image_Processing.Rmd

Overview

In this tutorial, we present a brief overview of image processing concepts necessary to understand machine learning and deep learning. This walk through was originally written in python: link to python version. We have tried to maintain functionality across both languages but certain libraries/features may only be available in one or the other. The basics of image processing should be the same across both.

This tutorial explores:

  • Loading image files into R
  • Printing properties of an image
  • Converting an image between color and grayscale
  • Identifying features (edges) within an image

Downloading Images

We will be using two images which can be downloaded from the following links:

cameraman.png peppers.png

From a terminal, we could have used the wget or curl commands to download the images.

wget https://geospatial.101workbook.org/tutorials/data/cameraman.png
wget https://geospatial.101workbook.org/tutorials/data/peppers.png

ls -1 *.png
#> cameraman.png
#> peppers.png

The cameraman.png on the left is in grayscale and the peppers.png on the right is in color. Processing color or grayscale images is slightly different, which we will explore in the following tutorial.

Loading images into R

We will assume you have a working R environment; however, see the following for a tutorial on setting up an R environment:

The nice thing about scripting languages is the fact that many tools are published as libraries. Which means you do not have to write your own functions from scratch. For this tutorial, we will be using R’s imager library available on CRAN (link to more info). There may be other image libraries more suited to your analysis, and we highly encourage you to explore, especially as new libraries are constantly being developed.

Below, we can install and load the imager library.

# install.packages("imager")       # <= uncomment to install from CRAN
library(imager)

From there, we can use the load.image function to read in cameraman.png. You may need the path to your input file, if they are not in the same location.

I_camera = load.image('data/cameraman.png')   # <= path to input image here
plot(I_camera)

Here, we have read in the image and stored it as I_camera. To verify that the image was successfully loaded into R, we have displayed the image using the plot function.

From the plot, notice how the x-axis goes from 0 to 300 from left to right. Strangely, the y-axis goes from 0 to 300, top to bottom. Therefore, the xy point (0,0) is actually the top left of the image. This can be very important as your analysis results may be different if the (0,0) is top left, right, bottom, or center. It’s a good idea to check where (0,0) is in the image.

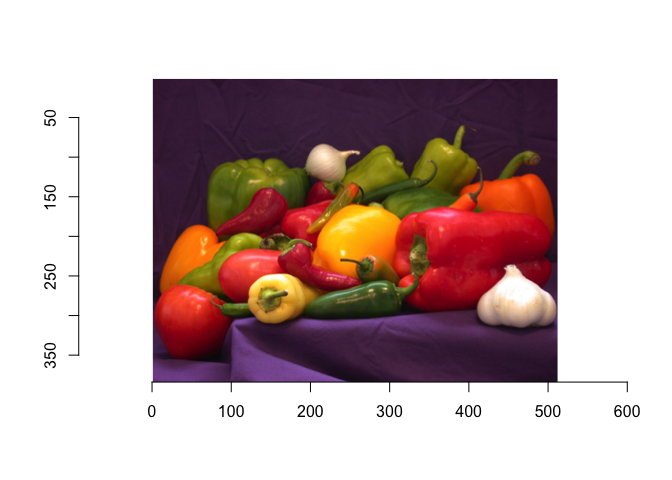
Now, we can also load the peppers.png in the same way, and store it as I_peppers.

I_peppers = load.image('data/peppers.png')   # <= path to input image here
plot(I_peppers)

Properties of an image

Now that we’ve loaded and plotted the images. What is an image object and its properties?

An image is actually stored as a matrix of pixels, usually stored in multiple layers. The diagram from https://media.geeksforgeeks.org/wp-content/uploads/Pixel.jpg is a good illustration of the concept of image layers.

image

From R, we can look at the structure (str) of a variable (I_camera) by the following:

str(I_camera)
#>  'cimg' num [1:256, 1:256, 1, 1] 0.612 0.624 0.62 0.608 0.62 ...

The structure of I_camera is an array of numbers cimg num [1:256, 1:256, 1, 1]. This is showing the dimension of the images to be 256 pixels wide, 256 pixels high, with 1 depth (layer), and 1 channel (because it’s a grayscale image).

Now, let’s look at I_peppers, which is a color image. How is the structure different?

str(I_peppers)
#>  'cimg' num [1:512, 1:384, 1, 1:3] 0.243 0.247 0.247 0.255 0.259 ...

Other then a 512 pixel width and 384 pixel height, notice how the 4th term is 1:3 which indicates three channels (RGB or Red Green Blue).

We could have also used the dimension (dim) function to quickly compare them.

dim(I_camera)        # Width_in_pixels Height_in_pixels Depth(layers) color(1=grayscale, 3=RGB)
#> [1] 256 256   1   1
dim(I_peppers)
#> [1] 512 384   1   3

Subregions of the image

Since an image object is really an R matrix, the matrix sub setting functions work to subset an image. Here, we pull out a subregion near the center of the image (100 to 110 pixels high and wide) and store it as sub_I_camera

sub_I_camera = as.cimg(I_camera[100:110,100:110,,] )
plot(sub_I_camera)

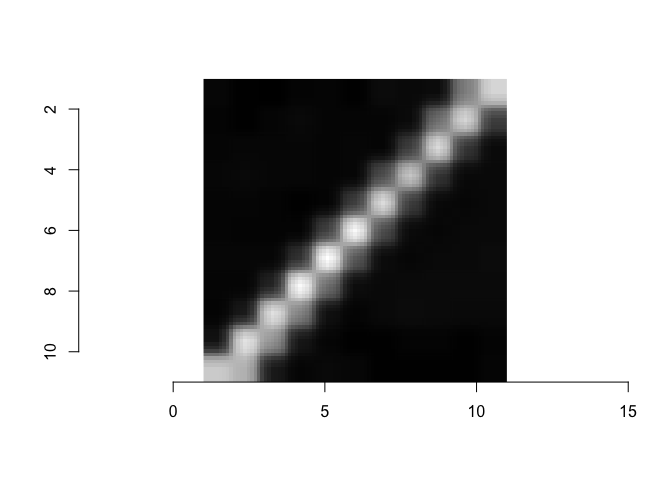
From this smaller sub_I_camera, we can print out the pixel values, get the minimum value and maximum value.

sub_I_camera[,,,1]
#>             [,1]       [,2]       [,3]       [,4]       [,5]       [,6]
#>  [1,] 0.04705882 0.03921569 0.04313725 0.04705882 0.04313725 0.04313725
#>  [2,] 0.03529412 0.03529412 0.04705882 0.05098039 0.04313725 0.03921569
#>  [3,] 0.03137255 0.04313725 0.04705882 0.04705882 0.03921569 0.03921569
#>  [4,] 0.03921569 0.05098039 0.04705882 0.04705882 0.03529412 0.03921569
#>  [5,] 0.04313725 0.04313725 0.04313725 0.04313725 0.03921569 0.27843137
#>  [6,] 0.03529412 0.04313725 0.04705882 0.04705882 0.27058824 0.78431373
#>  [7,] 0.06666667 0.04313725 0.04313725 0.32156863 0.71372549 0.31764706
#>  [8,] 0.05098039 0.06274510 0.27058824 0.65882353 0.26274510 0.05882353
#>  [9,] 0.06666667 0.41568627 0.70980392 0.23529412 0.05490196 0.04705882
#> [10,] 0.46274510 0.69803922 0.24313725 0.05490196 0.04705882 0.05490196
#> [11,] 0.69803922 0.26666667 0.05882353 0.05098039 0.05490196 0.05490196
#>             [,7]       [,8]       [,9]      [,10]      [,11]
#>  [1,] 0.04705882 0.04313725 0.03921569 0.10196078 0.67058824
#>  [2,] 0.04705882 0.04313725 0.13333333 0.72941176 0.60392157
#>  [3,] 0.04705882 0.18039216 0.72549020 0.52941176 0.12941176
#>  [4,] 0.22745098 0.78823529 0.47843137 0.11764706 0.04313725
#>  [5,] 0.80000000 0.41568627 0.09019608 0.04313725 0.05098039
#>  [6,] 0.35686275 0.07058824 0.03921569 0.03529412 0.04705882
#>  [7,] 0.06666667 0.05490196 0.05490196 0.03529412 0.03529412
#>  [8,] 0.04705882 0.06274510 0.06666667 0.03921569 0.03529412
#>  [9,] 0.05490196 0.05882353 0.06274510 0.03921569 0.03529412
#> [10,] 0.05490196 0.06274510 0.05098039 0.03529412 0.03529412
#> [11,] 0.06666667 0.06274510 0.05098039 0.03921569 0.04313725
min(sub_I_camera[,,,1])
#> [1] 0.03137255
max(sub_I_camera[,,,1])
#> [1] 0.8

See if you can subset and explore the I_peppers color image. Try to pull out a subimage that only contains one pepper.

Convert to Color Images to Grayscale

There are many reasons why we might want to convert a color image to a grayscale image. For one thing, it results in a reduction in image size (drop the 3 channels into 1). Another reason, is we want to focus on one color to identify an object in a busy scene. Or we may want to flatten certain layers to better identify edges of an object of interest.

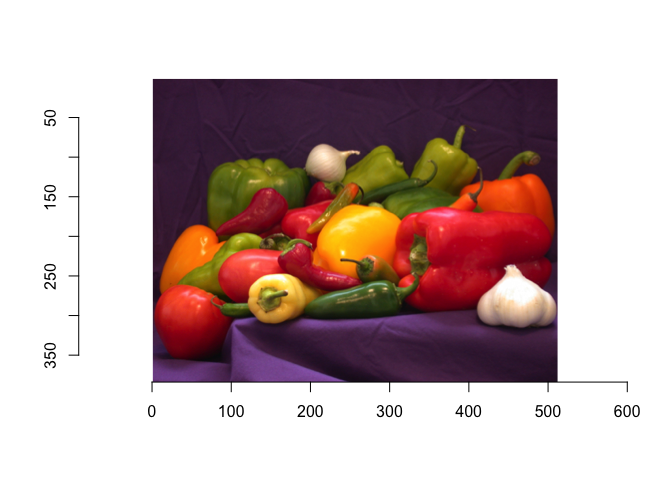
Recall the I_peppers color image?

I_peppers = load.image('data/peppers.png')       # <= path to peppers.png
plot(I_peppers)

The imager package provides a convenient grayscale function.

gray_I_peppers = grayscale(I_peppers)
plot(gray_I_peppers)

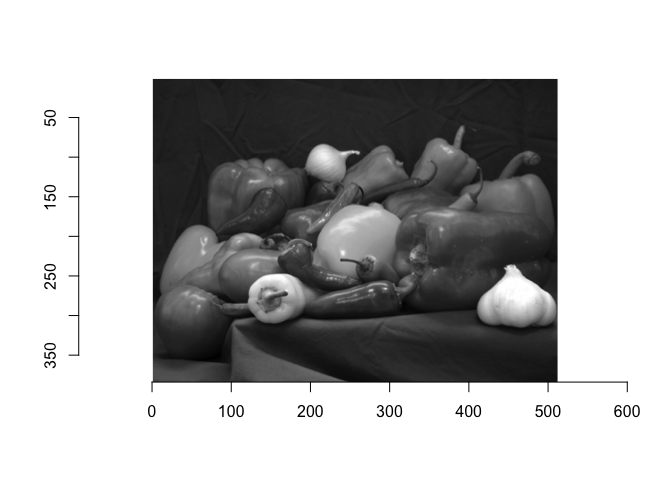
Recall that an image is really a matrix of numbers. Let’s compare the dimensions of the original with the new image.

dim(I_peppers)          # Color Original
#> [1] 512 384   1   3
dim(gray_I_peppers)     # Grayscale Transformed
#> [1] 512 384   1   1

The only difference should be the 4th entry.

Identify edge features in an image.

In order to identify objects in an image, it is often necessary to identify edges. While humans can intuitively identify edges to an object, computational edge detection is a bit more noisy. Usually it involves defining some gradiant function. An example shown below:

dx <- imgradient(I_camera, "x")
dy <- imgradient(I_camera, "y")
grad.mag <- sqrt(dx^2 + dy^2)
plot(grad.mag, main="Gradient magnitude")

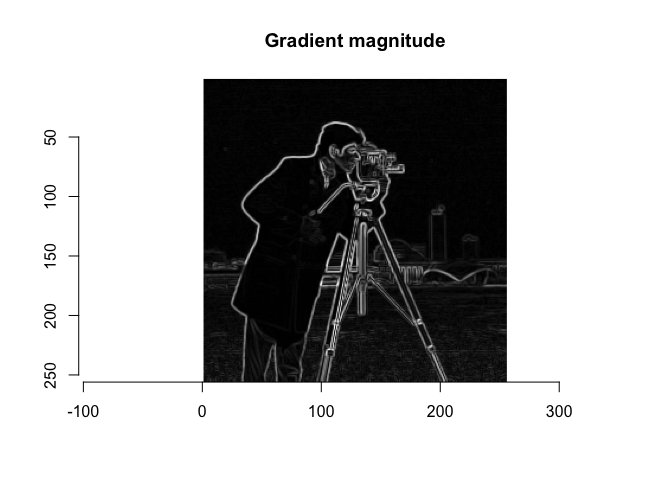
This particular function is called a Sobal Filter. To read more about Sobal filters, see this link: wikipedia - sobel operator

What happens if we identify edges in the color image I_peppers?

dx <- imgradient(I_peppers, "x")
dy <- imgradient(I_peppers, "y")
grad.mag <- sqrt(dx^2 + dy^2)
plot(grad.mag, main="Gradient magnitude")

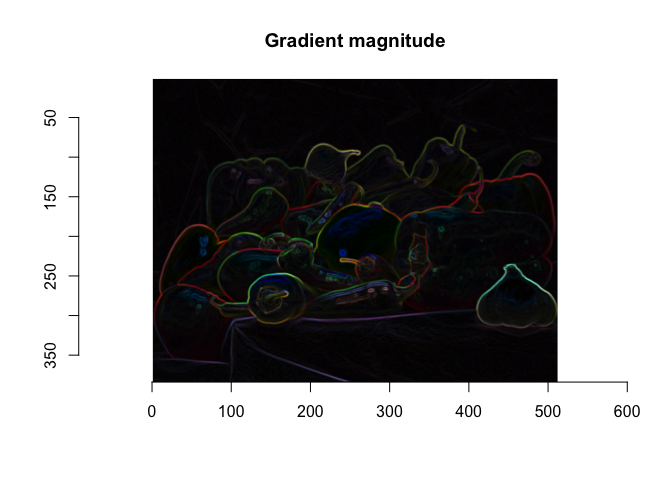
What happens if we convert the color image to a gray scale image first?

gray_I_peppers = grayscale(I_peppers)
dx <- imgradient(gray_I_peppers, "x")
dy <- imgradient(gray_I_peppers, "y")
grad.mag <- sqrt(dx^2 + dy^2)
plot(grad.mag, main="Gradient magnitude")

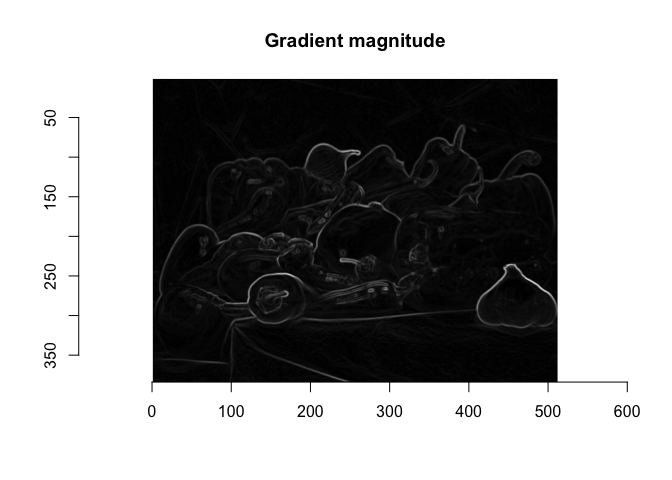
In Summary

Hopefully, you have learned how to:

  • load image files into R,
  • identify the dimensions of the image (gray vs color),
  • learned some common transformations (pull out subregions, convert to grayscale),
  • and identify edge features.

These colors and features can be fed into Machine Learning algorithms for image recognition such as but not limited to identifying roadways, forest cover, and snow cover. Hopefully, this has provided you with some intuition on how to perform analysis/transformations on image files.