Heather Savoy

Heather Savoy

Heather is a Computational Biologist (Data Scientist) in the USDA-ARS SCINet Office. Her research interests include applying informatics methods to multidisciplinary agro-ecosystem problems and building data science software tools for geospatial research. She received her Ph.D. in Civil and Environmental Engineering with an emphasis in Computational Data Science and Engineering from the University of California Berkeley. She also holds a B.S. in Environmental Science with a minor in Computational Mathematics from the Florida Institute of Technology.

Last Update: 4 January 2024
Download Jupyter Notebook: GRWG23_SpatialInterpolation_python.ipynb

Overview

This tutorial will implement and compare machine learning techniques with two approaches to including spatial proximity for spatial modeling tasks:

  • Spatial interpolation from point observations
  • Spatial prediction from point observations and gridded covariates

Language: Python

Primary Libraries/Packages:

Name Description Link
pandas Dataframes and other datatypes for data analysis and manipulation https://pandas.pydata.org/
geopandas Extends datatypes used by pandas to allow spatial operations on geometric types https://geopandas.org/en/stable/
scikit-learn Machine Learning in Python https://scikit-learn.org/stable/
plotnine A plotting library for Python modeled after R’s ggplot2 https://plotnine.readthedocs.io/en/v0.12.3/

Nomenclature

  • (Spatial) Interpolation: Using observations of dependent and independent variables to estimate the value of the dependent variable at unobserved independent variable values. For spatial applications, this can be the case of having point observations (i.e., variable observations at known x-y coordinates) and then predicting a gridded map of the variable (i.e., estimating the variable at the remaining x-y cells in the study area).
  • Random Forest: A supervised machine learning algorithm that uses an ensemble of decision trees for regression or classification.

Tutorial Steps

Step 0: Load libraries and define function

First, we will import required packages and set a large default figure size. We will also define a function to print model metrics.

from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score, mean_squared_error
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from scipy.stats import randint
import geopandas as gpd
import pandas as pd
import numpy as np
import plotnine as pn

pn.options.figure_size = (10, 10)

def print_metrics(y_test, y_pred):
    """
    Given observed and predicted y values, print the R^2 and RMSE metrics.

    y_test (Series): The observed y values.
    y_pred (Series): The predicted y values.
    """
    # R^2
    r2 = r2_score(y_test, y_pred)
    # Root mean squared error - RMSE
    rmse = mean_squared_error(y_test, y_pred, squared = False)
    print("R^2 = {0:3.2f}, RMSE = {1:5.0f}".format(r2,rmse))

Step 1: Read in and visualize point observations

We will open three vector datasets representing the point observations, the grid across which we want to predict, and the location of the river surrounding the study area.

This dataset gives locations and topsoil heavy metal concentrations, along with a number of soil and landscape variables at the observation locations, collected in a flood plain of the river Meuse, near the village of Stein (NL). Heavy metal concentrations are from composite samples of an area of approximately 15 m x 15 m. The data were extracted from the sp R package.

dnld_url = 'https://geospatial.101workbook.org/SpatialModeling/assets/'
# Point observations and study area grid
meuse_obs = gpd.read_file(dnld_url + 'meuse_obs.zip')
meuse_grid = gpd.read_file(dnld_url + 'meuse_grid.zip')

# Extra information for visualization:
xmin, ymin, xmax, ymax = meuse_grid.total_bounds
meuse_riv = gpd.read_file(dnld_url + 'meuse_riv.zip')

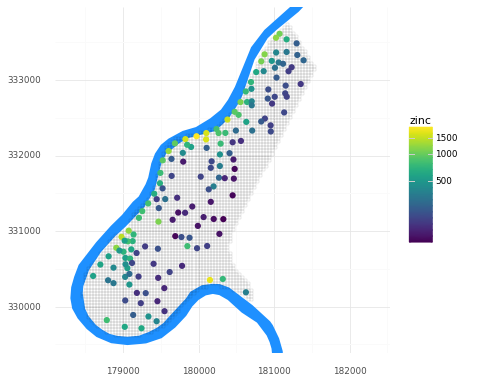
Let’s take a quick look at the dataset. Below is a map of the study area grid and the observation locations, plus the location of the river Meuse for reference. We can see that observed zinc concentrations tend to be higher closer to the river.

(pn.ggplot()
    + pn.geom_map(meuse_riv, fill = '#1e90ff', color = None)
    + pn.geom_map(meuse_grid, fill = None, size = 0.05)
    + pn.geom_map(meuse_obs, pn.aes(fill = 'zinc'), color = None, size = 3)
    + pn.scale_y_continuous(limits = [ymin, ymax]) 
    + pn.scale_fill_continuous(trans = 'log1p') 
    + pn.theme_minimal() 
    + pn.coord_fixed()
)

png

Step 2: Random Forest for spatial interpolation

We will explore two methods from recent literature that combine spatial proximity information as variables in fitting Random Forest models for spatial interpolation.

Step 2a: RFsp: distance to all observations

First, we will implement the RFsp method from Hengl et al 2018. This method involves using the distance to every observation as a predictor. For example, if there are 10 observations of the target variable, then there would be 10 predictor variables with the ith predictor variable representing the distance to the ith observation.

If you want to learn more about this approach, see the thengl/GeoMLA GitHub repo or the Spatial and spatiotemporal interpolation using Ensemble Machine Learning site from the same creators. Note: these resources are for R, but the latter does mention the scikit-learn library in Python that we will be using in this tutorial.

To start, we will generate two DataFrames of distances:

  • One with rows representing observations and columns representing observations (these will be our data for fitting and testing the model)
  • One with rows representing grid cell centers and columns representing observations (these will be how we estimate maps of our target variable with the final model)
# Get coordinates of grid cell centers - these are our locations at which we will
# want to interpolate our target variable.
grid_centers = meuse_grid.centroid

# Generate a grid of distances to each observation
grid_distances = pd.DataFrame()
# We also need the distance values among our observations
obs_distances = pd.DataFrame()

# We need a dataframe with rows representing prediction grid cells
# (or observations)
# and columns representing observations
for obs_index in range(meuse_obs.geometry.size):
    cur_obs = meuse_obs.geometry.iloc[obs_index]
    obs_name = 'obs_' + str(obs_index)
    
    cell_to_obs = grid_centers.distance(cur_obs).rename(obs_name)
    grid_distances = pd.concat([grid_distances, cell_to_obs], axis=1)

    obs_to_obs = meuse_obs.distance(cur_obs).rename(obs_name)
    obs_distances = pd.concat([obs_distances, obs_to_obs], axis=1)

Before moving on to model fitting, let’s take a look at the distance matrices we created.

obs_distances
obs_0 obs_1 obs_2 obs_3 obs_4 obs_5 obs_6 obs_7 obs_8 obs_9 ... obs_145 obs_146 obs_147 obs_148 obs_149 obs_150 obs_151 obs_152 obs_153 obs_154
0 0.000000 70.837843 118.848643 259.239272 366.314073 473.629602 258.321505 252.049598 380.189426 471.008492 ... 4304.014173 4385.565870 4425.191182 4194.974374 4077.205538 3914.407363 3868.323926 3964.443088 3607.233843 3449.821155
1 70.837843 0.000000 141.566239 282.851551 362.640318 471.199533 234.401365 195.010256 328.867755 441.530293 ... 4236.122756 4316.784220 4355.550137 4126.296645 4007.817486 3845.342247 3798.730841 3894.291848 3538.899546 3391.434505
2 118.848643 141.566239 0.000000 143.171226 251.023903 356.866922 167.000000 222.081066 323.513524 375.033332 ... 4278.052010 4365.122793 4411.447155 4173.908121 4061.434476 3896.201483 3854.403326 3956.156721 3584.262407 3389.963569
3 259.239272 282.851551 143.171226 0.000000 154.262763 242.156974 175.171345 296.786118 347.351407 322.818835 ... 4292.750750 4386.465206 4440.764349 4194.687712 4088.695146 3920.739726 3884.100024 3992.349935 3603.447377 3361.647959
4 366.314073 362.640318 251.023903 154.262763 0.000000 108.577162 147.526269 281.937936 266.101484 178.518907 ... 4162.607356 4260.340127 4319.896411 4068.314639 3966.640014 3796.976824 3763.871411 3876.723488 3476.475514 3212.786952
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
150 3914.407363 3845.342247 3896.201483 3920.739726 3796.976824 3786.887904 3753.359162 3676.331051 3579.912988 3620.842443 ... 471.958685 476.656060 536.660041 296.082759 183.619171 0.000000 147.989865 334.846233 345.144897 1443.022176
151 3868.323926 3798.730841 3854.403326 3884.100024 3763.871411 3757.931479 3714.900268 3633.511387 3540.952697 3589.008916 ... 599.736609 562.318415 557.046677 405.097519 217.082933 147.989865 0.000000 210.857772 391.256949 1545.369859
152 3964.443088 3894.291848 3956.156721 3992.349935 3876.723488 3875.800046 3821.201513 3734.408655 3647.002194 3703.768081 ... 702.359595 596.896138 497.033198 494.814107 276.524863 334.846233 210.857772 0.000000 595.131078 1756.173397
153 3607.233843 3538.899546 3584.262407 3603.447377 3476.475514 3462.718152 3438.127688 3365.864673 3265.476382 3299.412827 ... 702.659235 784.390209 880.273253 592.150319 528.674758 345.144897 391.256949 595.131078 0.000000 1176.606136
154 3449.821155 3391.434505 3389.963569 3361.647959 3212.786952 3163.395170 3225.188987 3198.113350 3071.672183 3038.833493 ... 1461.677119 1666.870721 1877.419772 1521.862017 1600.647681 1443.022176 1545.369859 1756.173397 1176.606136 0.000000

155 rows × 155 columns

For fitting our model, we will use the distances among observations as our predictors and observed zinc concentration at those observations as our target variable.

# matrix of distance to observations as predictors
RFsp_X = obs_distances
# vector of observed zinc concentration as target variable
y = meuse_obs['zinc']

# We need to split our dataset into train and test datasets. We'll use 80% of
# the data for model training.
RFsp_X_train, RFsp_X_test, RFsp_y_train, RFsp_y_test = train_test_split(RFsp_X, y, train_size=0.8)

Machine learning algorithms typically have hyperparameters that can be tuned per application. Here, we will tune the number of trees in the random forest model and the maximum depth of the trees in the the random forest model. We use the training subset of our data for this fitting and tuning process. After the code chunk below, the best parameter values from our search are printed.

r_state = 0

# Define the parameter space that will be searched over.
param_distributions = {'n_estimators': randint(1, 100),
                       'max_depth': randint(5, 10)}

# Now create a searchCV object and fit it to the data.
tuned_RFsp = RandomizedSearchCV(estimator=RandomForestRegressor(random_state=r_state),
                            n_iter=10,
                            param_distributions=param_distributions,
                            random_state=r_state).fit(RFsp_X_train, RFsp_y_train)
tuned_RFsp.best_params_

{'max_depth': 7, 'n_estimators': 37}

We can now use our testing subset of the data to quantify the model performance, i.e. how well did the model predict the remaining observed values? There are many potential metrics - see all the metrics scikit-learn supports here. The two we show below are the coefficient of determination (R2) and the root mean square error (RMSE), two metrics that are likely familiar from outside machine learning as well.

print_metrics(RFsp_y_test, tuned_RFsp.predict(RFsp_X_test))

R^2 = 0.50, RMSE =   286

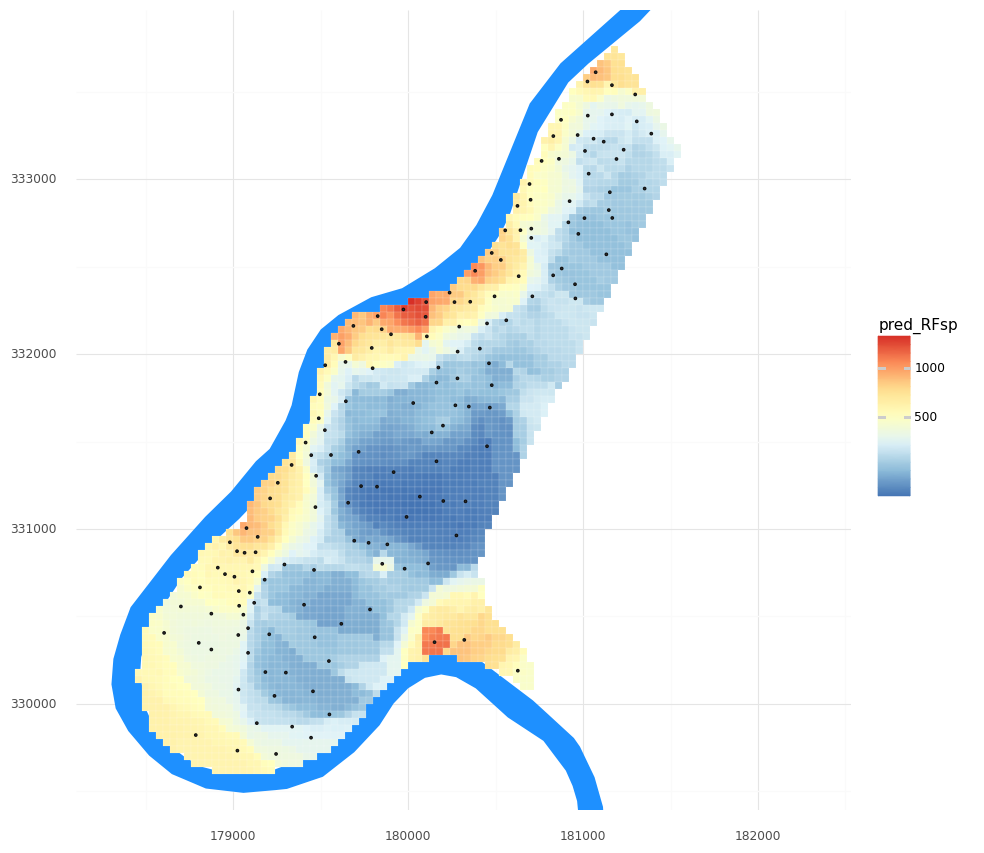
Our R2 is not awesome! We typically want R2 values closer to 1 and RMSE values closer to 0. Note: RMSE is in the units of the target variable, so our zinc concentrations. You can see the range of values of zinc concentrations in the legend in the figure above, from which you can get a sense of our error.

Excercise: Modify the param_distributions and n_iter values above - can you improve the metrics? Note that you may also increase the processing time.

Once we are happy with (or at least curious about!) the model, we can predict and visualize our zinc concentration field.

# Predict the value from all grid cells using their distances we determined above. 
meuse_grid['pred_RFsp'] = tuned_RFsp.predict(grid_distances)

(pn.ggplot()
    + pn.geom_map(meuse_riv, fill = '#1e90ff', color = None)
    + pn.geom_map(meuse_grid, pn.aes(fill = 'pred_RFsp'), color = 'white', size = 0.05)
    + pn.geom_map(meuse_obs)
    + pn.scale_y_continuous(limits = [ymin, ymax]) 
    + pn.scale_fill_distiller(type = 'div', palette = 'RdYlBu',trans = 'log1p') 
    + pn.theme_minimal() 
    + pn.coord_fixed()
)

png

2b: RFSI: n observed values and distance to those n observation locations

Now, we will try the the RFSI method from Sekulić et al 2020. In this method, instead of using distances to all observations as our predictors, we will use distances to the n closest observations as well as the observed values at those locations as our predictors.

Below, we define a function to find the n closest observations and record their distances and values.

def nclosest_dist_value(dist_ij, obs_i, n = 3):
    """
    Given a distance matrix among i locations and j observation 
    locations, j observed values, and the number of close
    observations desired, generates a dataframe of distances to
    and values at n closest observations for each of the i 
    locations.

    dist_ij (DataFrame): distance matrix among i locations and j 
    observation locations
    obs_i (Series): The i observed values
    n (int): The desired number of closest observations
    """
    # Which observations are the n closest? 
    # But do not include distance to oneself. 
    # Note: ranks start at 1, not 0.
    nclosest_dist_ij =  dist_ij.replace(0.0,np.nan).rank(axis = 1, method = 'first') <= n
    
    nclosest = pd.DataFrame()

    # For each observation, find the n nearest observations and
    # record the distance and target variable pairs
    for i in range(dist_ij.shape[0]):
        # Which obs are the n closest to the ith location?
        nclosest_j_indices = np.where(nclosest_dist_ij.iloc[i,:])

        # Save the distance to and observed value at the n closest
        # observations from the ith location
        i_loc_dist = dist_ij.iloc[i].iloc[nclosest_j_indices]
        sort_indices = i_loc_dist.values.argsort()
        i_loc_dist = i_loc_dist.iloc[sort_indices]
        i_loc_dist.rename(lambda x: 'dist' + str(np.where(x == i_loc_dist.index)[0][0]), inplace=True)
        
        i_loc_value = obs_i.iloc[nclosest_j_indices]
        i_loc_value = i_loc_value.iloc[sort_indices]
        i_loc_value.rename(lambda x: 'obs' + str(np.where(x == i_loc_value.index)[0][0]), inplace=True)
        i_loc = pd.concat([i_loc_dist,i_loc_value],axis = 0)
        nclosest = pd.concat([nclosest, pd.DataFrame(i_loc).transpose()], axis = 0)

    return nclosest

Let’s now use that function to find and describe the n closest observations to each obsersevation and each grid cell. Note that we are taking advantage of the obs_distances and grid_distances variables we created for the RFsp approach.

n = 10
obs_nclosest_obs = nclosest_dist_value(obs_distances, meuse_obs['zinc'], n)
grid_nclosest_obs = nclosest_dist_value(grid_distances, meuse_obs['zinc'], n)

Let’s take a closer look at our new distance matrices.

obs_nclosest_obs
dist0 dist1 dist2 dist3 dist4 dist5 dist6 dist7 dist8 dist9 obs0 obs1 obs2 obs3 obs4 obs5 obs6 obs7 obs8 obs9
0 70.837843 118.848643 252.049598 258.321505 259.239272 336.434243 366.314073 373.483601 380.189426 399.656102 1141.0 640.0 406.0 346.0 257.0 1096.0 269.0 504.0 347.0 279.0
0 70.837843 141.566239 195.010256 234.401365 266.011278 282.851551 311.081983 328.867755 356.349547 362.640318 1022.0 640.0 406.0 346.0 1096.0 257.0 504.0 347.0 279.0 269.0
0 118.848643 141.566239 143.171226 167.000000 222.081066 251.023903 323.513524 326.401593 345.891602 351.973010 1022.0 1141.0 257.0 346.0 406.0 269.0 347.0 279.0 504.0 1096.0
0 143.171226 154.262763 175.171345 242.156974 259.239272 282.851551 296.786118 322.818835 324.499615 347.351407 640.0 269.0 346.0 281.0 1022.0 1141.0 406.0 183.0 279.0 347.0
0 108.577162 147.526269 154.262763 178.518907 221.758878 244.296950 251.023903 266.101484 281.937936 340.847473 281.0 346.0 257.0 183.0 279.0 189.0 640.0 347.0 406.0 326.0
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
0 117.038455 145.602198 147.989865 183.619171 217.117480 262.619497 269.818457 293.400750 296.082759 334.846233 224.0 189.0 496.0 214.0 187.0 400.0 296.0 154.0 258.0 342.0
0 116.361506 141.000000 147.989865 160.863296 210.857772 217.082933 219.665655 243.772435 273.791892 287.702972 400.0 296.0 166.0 187.0 342.0 214.0 539.0 224.0 451.0 332.0
0 81.412530 174.942848 205.000000 210.857772 242.866218 270.351623 276.524863 286.225436 296.278585 301.317109 332.0 400.0 420.0 496.0 296.0 539.0 214.0 553.0 451.0 577.0
0 158.294030 170.390727 195.747286 260.555176 260.823695 309.161770 345.144897 353.747085 384.532183 385.020779 155.0 199.0 180.0 187.0 224.0 154.0 166.0 157.0 296.0 226.0
0 353.004249 503.135171 799.335974 848.958185 870.917907 914.617406 986.887025 1013.126349 1038.171469 1043.985153 722.0 1672.0 192.0 130.0 203.0 157.0 778.0 113.0 240.0 199.0

155 rows × 20 columns

We will then use the same model fitting process as for RFsp.

# matrix of distances to and observed values at the n closest observations as predictors
RFSI_X = obs_nclosest_obs

# We need to split our dataset into train and test datasets. We'll use 80% of
# the data for model training.
RFSI_X_train, RFSI_X_test, RFSI_y_train, RFSI_y_test = train_test_split(RFSI_X, y, train_size=0.8)

param_distributions = {'n_estimators': randint(1, 100),
                       'max_depth': randint(5, 10)}
tuned_RFSI  = RandomizedSearchCV(estimator=RandomForestRegressor(random_state=r_state),
                            n_iter=10,
                            param_distributions=param_distributions,
                            random_state=r_state).fit(RFSI_X_train, RFSI_y_train)
tuned_RFSI.best_params_


{'max_depth': 9, 'n_estimators': 59}

print_metrics(RFSI_y_test, tuned_RFSI.predict(RFSI_X_test))

R^2 = 0.45, RMSE =   302

How does RFSI’s metrics compare to RFsp’s? What if you modify n, the number of closest observations? What if you modify the param_distributions and n_iter values like above?

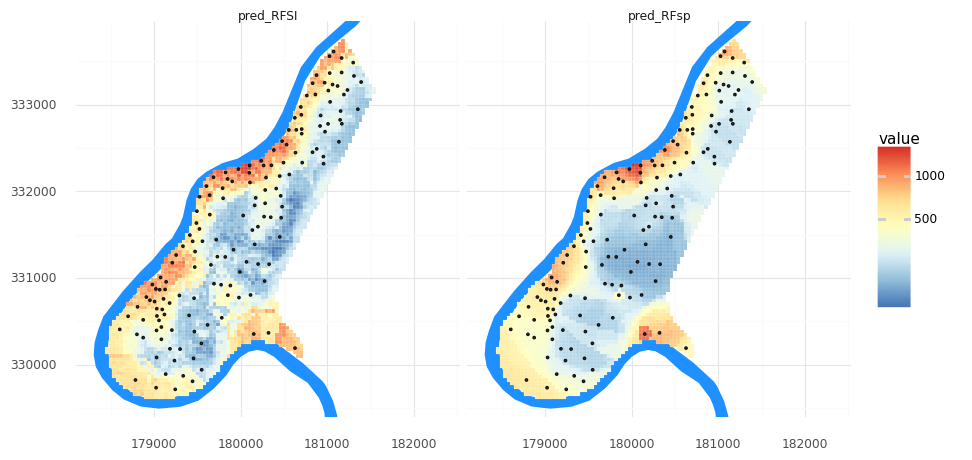
Let’s visualize the two maps from these two methods together. To do so, we will need to transform our meuse_grid DataFrame into a longer format for plotting with facets in plotnine.

meuse_grid['pred_RFSI'] = tuned_RFSI.predict(grid_nclosest_obs)
meuse_grid_long = pd.melt(meuse_grid, id_vars= 'geometry', value_vars=['pred_RFsp','pred_RFSI'])

(pn.ggplot()
    + pn.geom_map(meuse_riv, fill = '#1e90ff', color = None)
    + pn.geom_map(meuse_grid_long, pn.aes(fill = 'value'), color = 'white', size = 0.05)
    + pn.geom_map(meuse_obs)
    + pn.scale_y_continuous(limits = [ymin, ymax]) 
    + pn.scale_fill_distiller(type = 'div', palette = 'RdYlBu',trans = 'log1p') 
    + pn.theme_minimal() 
    + pn.coord_fixed() 
    + pn.facet_wrap('variable')
)

png

Step 3: Bringing in gridded covariates

This dataset has three covariates supplied with the grid and the observations:

  • dist: the distance to the river
  • ffreq: a category describing the flooding frequency
  • soil: a category of soil type

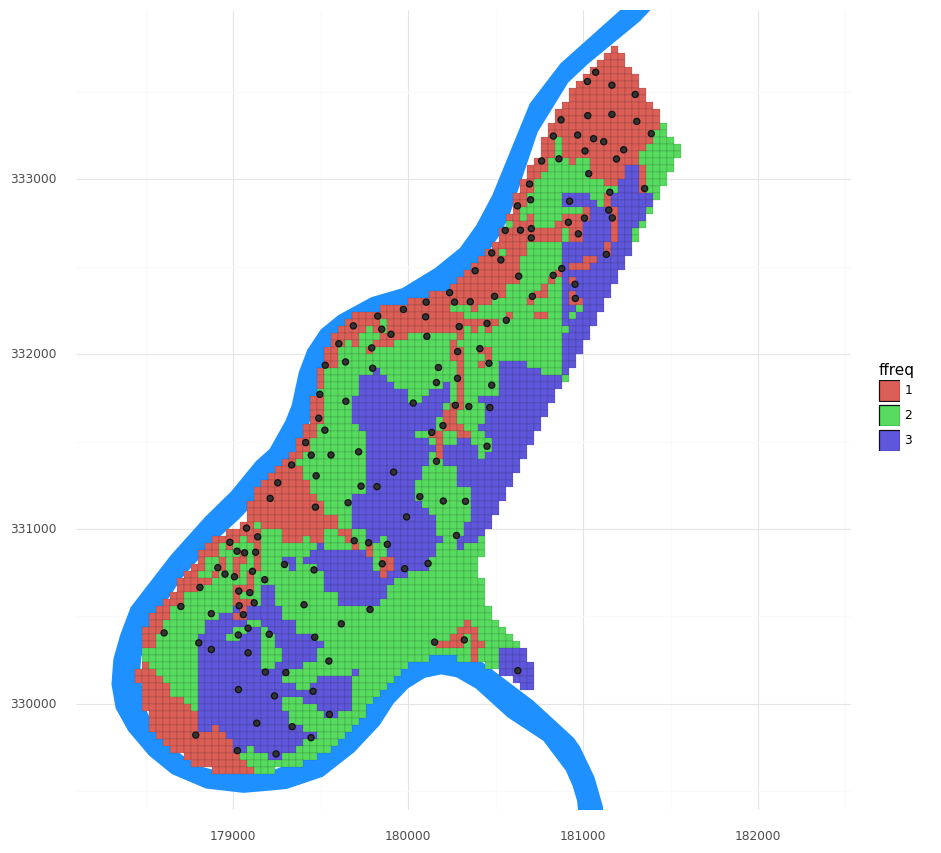
We can extend this spatial interpolation task into a more general spatial prediction task by including these co-located observations and gridded covariates. Let’s visualize the flooding frequency:

(pn.ggplot()
    + pn.geom_map(meuse_riv, fill = '#1e90ff', color = None)
    + pn.geom_map(meuse_grid, pn.aes(fill = 'ffreq'), size = 0.05)
    + pn.geom_map(meuse_obs, size = 2)
    + pn.scale_y_continuous(limits = [ymin, ymax]) 
    + pn.theme_minimal() 
    + pn.coord_fixed()
)

png

Also visualize the other covariates. (Either one at a time, or try melting like above to use facets!). Do you expect these variables to improve the model?

Adding these covariates to the RF model, either method, is straightforward. We will stick to just the RFSI model here. All that needs to be done is to concatenate these three columns to our distance (and observed values) dataset and repeat the modeling fitting process.

# matrix of distances to and observed values at the n closest observations as predictors
RFSI_wcov_X = pd.concat([obs_nclosest_obs.reset_index(),meuse_obs[['dist','ffreq','soil']]], axis=1)

# We need to split our dataset into train and test datasets. We'll use 80% of
# the data for model training.
RFSI_wcov_X_train, RFSI_wcov_X_test, RFSI_wcov_y_train, RFSI_wcov_y_test = train_test_split(RFSI_wcov_X, y, train_size=0.8)

param_distributions = {'n_estimators': randint(1, 100),
                       'max_depth': randint(5, 10)}
tuned_RFSI_wcov = RandomizedSearchCV(estimator=RandomForestRegressor(random_state=r_state),
                            n_iter=10,
                            param_distributions=param_distributions,
                            random_state=r_state).fit(RFSI_wcov_X_train, RFSI_wcov_y_train)
tuned_RFSI_wcov.best_params_

{'max_depth': 5, 'n_estimators': 68}

print_metrics(RFSI_wcov_y_test, tuned_RFSI_wcov.predict(RFSI_wcov_X_test))

R^2 = 0.56, RMSE =   260

How did the new covariates change our metrics? Was it as you’d expect?

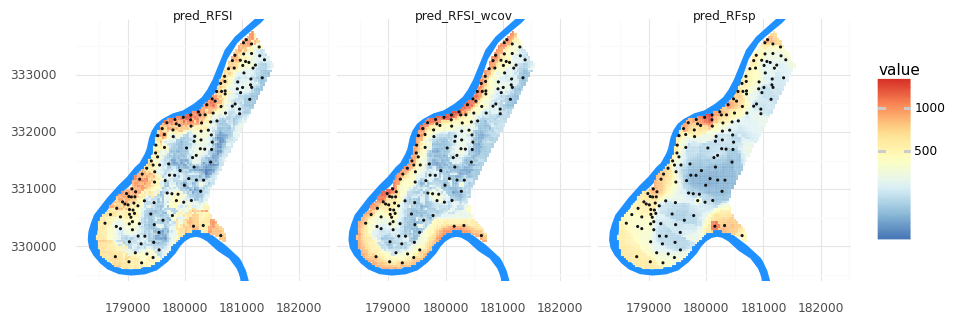
grid_nclosest_obs_wcov = pd.concat([grid_nclosest_obs.reset_index(),meuse_grid[['dist','ffreq','soil']]], axis=1)
meuse_grid['pred_RFSI_wcov'] = tuned_RFSI_wcov.predict(grid_nclosest_obs_wcov)

meuse_grid_long = pd.melt(meuse_grid, id_vars= 'geometry', value_vars=['pred_RFsp','pred_RFSI','pred_RFSI_wcov'])


(pn.ggplot()
    + pn.geom_map(meuse_riv, fill = '#1e90ff', color = None)
    + pn.geom_map(meuse_grid_long, pn.aes(fill = 'value'), color = 'white', size = 0.05)
    + pn.geom_map(meuse_obs, size = 0.25)
    + pn.scale_y_continuous(limits = [ymin, ymax]) 
    + pn.scale_fill_distiller(type = 'div', palette = 'RdYlBu',trans = 'log1p') 
    + pn.theme_minimal() 
    + pn.coord_fixed() 
    + pn.facet_wrap('variable')
)

png

Use the covariates to create a RFsp_wcov model and add it to the figure. How do the metrics compare to the other results?